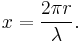Light scattering by particles

Light scattering by particles is the process by which small particles such as ice crystals, dust, planetary dust, and blood cells cause observable phenomena such as rainbows, the color of the sky, and halos.

Maxwell's equations are the basis of theoretical and computational methods describing light scattering but since exact solutions to Maxwell's equations are only known for selected geometries (such as spherica particle) light scattering by particles is a branch of computational electromagnetics dealing with electromagnetic radiation scattering and absorption by particles.

In case of geometries for which analytical solutions are known (such as spheres, cluster of spheres, infinite cylinders), the solutions are typically calculated in terms of infinite series. In case of more complex geometries and for inhomogeneous particles the original Maxwell's equations are discretized and solved. Multiple-scattering effects of light scattering by particles are treated by radiative transfer techniques (see, e.g. atmospheric radiative transfer codes).

Relative size of a scattering particle is defined by size parameter which is the ratio of its characteristic dimension and wavelength

x = \frac{2 \pi r} {\lambda}.

Contents

Exact Computational methods

Mie approximation

Main article: Mie theory

Scattering from any spherical particles with arbitrary size parameter is explained by the Mie theory. Mie theory, also called Lorenz-Mie theory or Lorenz-Mie-Debye theory, is a complete analytical solution of Maxwell's equations for the scattering of electromagnetic radiation by spherical particles (Bohren and Huffman, 1998).

For more complex shapes such as coated spheres, multispheres, spheroids, and infinite cylinders there are extensions which express the solution in terms of infinite series.

Discrete dipole approximation

Main article: Discrete dipole approximation

There are several techniques for computing scattering of radiation by particles of arbitrary shape. The discrete dipole approximation is an approximation of the continuum target by a finite array of polarizable points. The points acquire dipole moments in response to the local electric field. The dipoles of these points interact with one another via their electric fields.

T-matrix

Main article: T-matrix_method

The technique is also known as null field method and extended boundary technique method (EBCM). Matrix elements are obtained by matching boundary conditions for solutions of Maxwell equations. The incident, transmitted, and scattered field are expanded into spherical vector wave functions.

Finite-difference time-domain method

Main article: Finite-difference time-domain method

The FDTD method belongs in the general class of grid-based differential time-domain numerical modeling methods. The time-dependent Maxwell's equations (in partial differential form) are discretized using central-difference approximations to the space and time partial derivatives. The resulting finite-difference equations are solved in either software or hardware in a leapfrog manner: the electric field vector components in a volume of space are solved at a given instant in time; then the magnetic field vector components in the same spatial volume are solved at the next instant in time; and the process is repeated over and over again until the desired transient or steady-state electromagnetic field behavior is fully evolved.

Approximate methods

Approximation Refractive index Size parameter Phase shift
Rayleigh scattering abs(mx) very small very small
Geometric optics very large very large
Anomalous Diffraction Theory abs(m-1) very small x large
Complex Angular Momentum moderate m large x

Rayleigh scattering

Rayleigh scattering regime is the scattering of light, or other electromagnetic radiation, by particles much smaller than the wavelength of the light. Rayleigh scattering can be defined as scattering in small size parameter regime 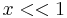x << 1 .

Geometric optics

Main article: Geometric optics

See also

References